虚数i自诞生以来就给数学界带来了巨大的震撼和启发,它在解决实数中无法解决的问题上发挥了重要作用。本文将围绕虚数i的运算公式展开讨论,并探索其在数学中的应用。

1.虚数的定义和性质:从根源上来说,虚数i就是定义为满足$i^2=-1$的一种特殊数。虚数有其独特的性质,如乘方、加减法等。
2.虚数的运算规则:虚数的运算规则是通过定义来确定的,如虚数与实数的乘法规则、虚数之间的加减法规则等。

3.复数的表示形式:复数可以用代数形式$a+bi$表示,其中$a$为实部,$b$为虚部。复数有着独特的几何解释,即复平面上的点。
4.复数的共轭:复数的共轭是指保持实部不变而虚部取负的操作,可以用来求复数的模。
5.复数的乘法运算:复数的乘法运算是通过将虚数单位$i$的乘方性质应用于复数的每一个部分,然后进行简化得到结果。
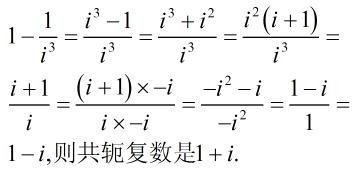
6.复数的除法运算:复数的除法运算可以通过将分子和分母同时乘以分母的共轭得到,然后进行简化得到结果。
7.虚数单位i的应用:虚数单位i在物理学和工程学中有着广泛的应用,如交流电学、电磁场理论等。
8.欧拉公式:欧拉公式是数学中一个重要的公式,将复数与三角函数之间建立了联系,具有深远的意义。
9.应用于解方程:虚数i在解一些复杂方程时起到了关键的作用,它能够让原本无解的方程变为有解的方程。
10.应用于几何图形:虚数i在几何图形的表示和变换中起到了重要的作用,如旋转、缩放等操作。
11.应用于信号处理:虚数i在信号处理领域中有着广泛的应用,如频率域分析、滤波等。
12.应用于量子力学:虚数i在量子力学中是不可或缺的,它是描述量子力学中粒子波函数的基础。
13.应用于图像处理:虚数i在图像处理中可以用来表示和操作图像的相位信息,如边缘检测、滤波等。
14.应用于控制工程:虚数i在控制工程中可以用来描述系统的稳定性和动态响应,如根轨迹法、频率响应等。
15.虚数i作为一种特殊的数,它的引入使得无法解决的问题得以解决,并在数学以及相关领域中发挥着重要作用。掌握虚数i的运算公式和应用将有助于我们更好地理解和应用数学知识。